Whitening (Statistik)

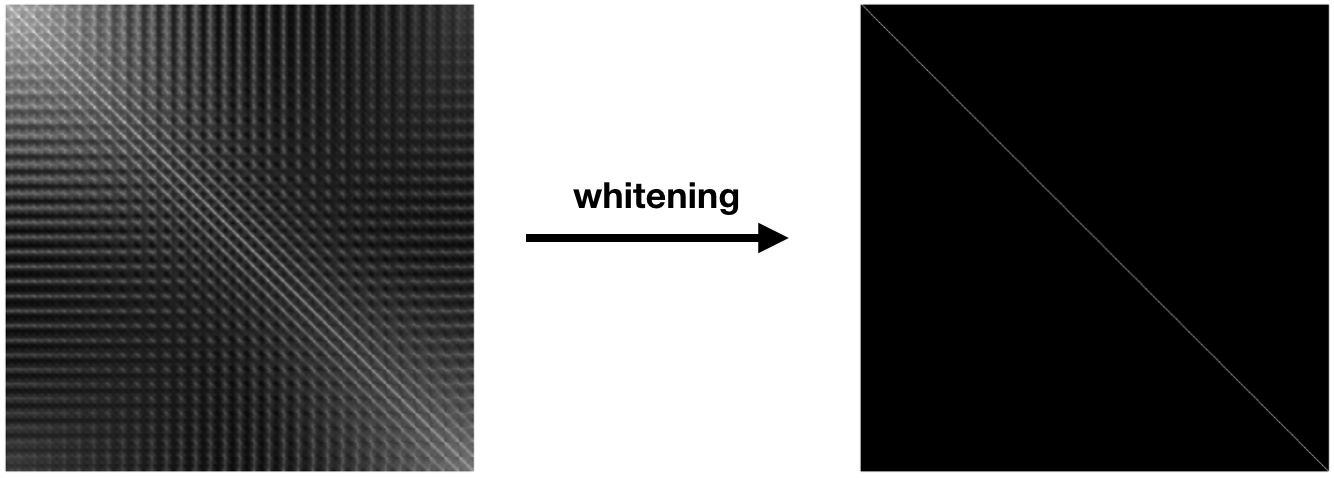
Die Whitening-Transformation bezeichnet eine lineare Transformation, bei der ein Vektor von Zufallsvariablen mit bekannter Kovarianzmatrix in eine Reihe von neuen Variablen umgewandelt wird, deren Kovarianzmatrix der Einheitsmatrix gleicht. Angestrebt wird ein Zustand, in dem die einzelnen Variablen unkorreliert sind und jeweils eine Varianz von 1 haben. Die Transformation wird als „Whitening“ bezeichnet, da nach der Umwandlung die Verteilungseigenschaften des Inputvektors denen des Weißen Rauschens entsprechen. Ziel ist eine Stetige Gleichverteilung.

Einige andere Transformationen stehen in enger Beziehung zum Whitening:

1. die Dekorrelationstransformation entfernt nur Korrelationen aber lässt die Varianzen intakt,
2. die Standardisierungstransformation setzt die Varianzen 1 aber lässt die Korrelationen intakt,
3. die Coloring-Transformation übersetzt einen Vektor mit „weißen“ Zufallsvariablen in einen Zufallsvektor mit einer spezifischen Kovarianzmatrix.

Definition

Angenommen ${\displaystyle X}$ ist ein Zufalls-Spalten-Vektor mit nicht-singulärer Kovarianzmatrix ${\displaystyle M}$und Mittelwert ${\displaystyle 0}$. Dann führt die Transformation ${\displaystyle Y=WX}$mit einer Whitening-Matrix ${\displaystyle W}$, welche die Bedingung ${\displaystyle W^{\mathrm {T} }W=M^{-1}}$ erfüllt, zu einem „whitened“ Zufallsvektor ${\displaystyle Y}$mit einheitlicher diagonaler Kovarianz.

Es gibt eine unendliche Anzahl möglicher Whitening-Matrizen ${\displaystyle W}$. Gebräuchliche Auswahlen sind ${\displaystyle W=M^{-1/2}}$ (Mahalanobis or ZCA whitening), die Cholesky-Zerlegung von ${\displaystyle M^{-1}}$ (Cholesky whitening) oder die Eigenvektoren von ${\displaystyle M}$ (PCA whitening).

Kessy et al. (2018) demonstrieren, dass optimale Whitening-Transformationen durch Untersuchen der Kreuzvarianzen und Kreuzkorrelationen von ${\displaystyle X}$und ${\displaystyle Y}$erkannt werden können. Zum Beispiel, die singuläre optimale Whitening-Transformation zum Erreichen der maximalen komponentenweisen Korrelation zwischen dem ursprünglichen ${\displaystyle X}$ und geweißten ${\displaystyle Y}$ wird durch die Whitening-Matrix ${\displaystyle W=P^{-1/2}V^{-1/2}}$ erzeugt. Hierbei ist ${\displaystyle P}$ die Korrelationsmatrix und ${\displaystyle V}$ die Varianzmatrix.

Eine Datenmatrix „weißen“

Das Whitening einer Datenmatrix folgt den gleichen Transformationen wie Zufallsvariablen. Eine empirische Whitening-Transformation erfolgt durch die Schätzung der Kovarianz (z. B. durch die Maximum-Likelihood-Methode) und anschließender Konstruktion einer entsprechend geschätzten Whitening-Matrix (z. B. durch die Cholesky-Zerlegung).

Siehe auch

• Hauptkomponentenanalyse
• Kanonische Korrelation
• Symmetrische Orthogonalisierung

Weblinks

• courses.media.mit.edu (PDF)
• The ZCA whitening transformation. (PDF; 4,0 MB) Appendix A von A. Krizhevsky: Learning Multiple Layers of Features from Tiny Images.

Einzelnachweise